On January 6th, 2005, a freight train moving northbound through Graniteville, South Carolina, intersected a railroad switch set in the wrong position. The train was directed into an industrial siding and collided with a parked train, derailing 3 locomotives and 17 freight cars – three of which contained chlorine gas. One of the chlorine tanks ruptured and killed 9 people, injured 554, and temporarily displaced 5,400 residents living within a 1-mile radius of the accident1.
The Graniteville collision was just one of many fatal train accidents that occurred over the past decade. In 2008, after another deadly collision in Chatsworth, California2, the government intervened and passed the Rail Safety Improvement Act (RSIA). The RSIA requires all Class I railroads carrying passengers or toxic-by-inhalation (TIH) materials to be equipped with Positive Train Control (PTC) technologies3. PTC systems prevent accidents by detecting and warning train crews of impending hazards, and by automatically stopping the train if necessary.
Final regulations published in 2010 required affected railroads to demonstrate through a risk assessment that their proposed PTC technology would provide at least an 80% reduction in risk over their existing system. To ensure that assessments were reliable, the Federal Railroad Administration (FRA) hired our firm, DecisionTek, to investigate methods for evaluating the inherent safety risk of rail systems. Given any rail territory, our challenge was to predict train accidents over its life cycle, with and without PTC technology, and to assess whether the rail operator’s PTC implementation on the territory provided a sufficient degree of additional safety.
How to predict train accidents
Train accidents are rare. They are also highly dependent of the territories on which they occur, specifically the territories’ track topology and operating environment. As a result, predictions for accident frequency cannot be based solely on empirical data, and must instead be determined using simulation analysis.
Ideally, we would simulate hundreds of years of train operations on a modeled territory that closely replicates ours of study, and generate a sufficient number of accidents on the territory to derive statistically significant estimates for their frequency. Such a simulation would take into account the physical characteristics of the territory (e.g. track connections, grades, curvatures, and speed zones) and its traffic conditions (e.g. train equipment, timetables, and schedules), and would incorporate human errors and equipment failures that lead to train accidents. I helped to develop the simulation software that does exactly this.
However, our simulator had to overcome a big drawback of using traditional simulation methods (e.g. Monte Carlo) to predict rare events. Simulating railroad operations is computationally intensive; even when deployed on a 12-core high-performance server, our software required 22 seconds to simulate one day of operations on a low-traffic territory. If 1,000 years of simulated operations were required to generate statistically reliable estimates of accident frequency, our software would need 93 days to perform the analysis. To address this problem, we devised a simulation technique that employs the concept of multi-level splitting4.
Multi-level splitting for rare-event simulation
The idea of multi-level splitting is to break the simulation process into several successive stages, where each stage generates events that are increasingly likely to lead to accidents or incidents.
In our implementation, the first stage focuses on generating human errors or equipment failures. When those events occur in a simulation, the software pauses, freezes the current state (i.e. serializes all objects in memory), stores the state in the database, then resumes the simulation. After capturing a sufficient number of events, the second simulation stage can begin.
In the second stage, the software randomly selects, unserializes, and resumes states that were stored in the first stage. Because each selected simulation state contains an error or failure event, simulations in the second stage are more likely to generate accident events. However, because accidents are still too difficult to generate at this point, in this stage we focus on generating hazardous events. Some of these include when trains exceed their authority (i.e. “burn a red light”), overspeed, or intersect a switch that is set in the wrong position. When such events occur, again, the system state is recorded and stored for use in the following stage.
The third and final stage randomly selects from events stored in the second stage and resumes them from the point at which they were stored. This stage seeks to generate accident or incident events, such as collisions or derailments, and is more likely to generate them because all simulations begin from a hazardous situation. When accidents occur, specifics such as train identification, time, location, and speed are recorded and the simulation for that selected sample terminates. The stage terminates when a sufficient number of accidents are generated to obtain a reliable estimate for their frequency.
The math behind multi-level splitting
Each simulation stage is performed separately and requires unique simulation parameters. When simulating the first stage, users define railroad infrastructure and operational data, some period of analysis (e.g. January 1st, 2013 through December 31st, 2038), and reliability rates for human errors and equipment failures. Without parallel processing, the simulation can take up to two days for a typical 25-year period. During this time, the simulation can generate a set of human errors and equipment failures that are diverse-enough to lead to every possible accident or incident event.
When the simulation terminates, we can calculate the mean time to error or failure using the equation:
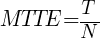 , where T is the period of analysis and N is the number of errors or failures generated.
, where T is the period of analysis and N is the number of errors or failures generated.
When running the next simulation stage, users select a stage 1 simulation result and specify the number of times they would like to sample from its events. Each “trial” is a simulation that begins from a stage 1 event (i.e. human error or equipment failure) and that can lead either to a hazardous event or to a safe resolution. A small number of trials may not be sufficient to generate all possible hazardous situations, whereas an excessively large number of trials may waste computer resources by generating duplicate events after exhausting all possible paths.
When the stage 2 simulation completes, we can calculate the probability of a hazardous event given an error or failure using the following formula:
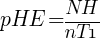 , where NH is the number of hazardous events generated in the second stage and nT1 is the number of trials used to generate those events.
, where NH is the number of hazardous events generated in the second stage and nT1 is the number of trials used to generate those events.
This value is then used to calculate the mean time to hazardous event, defined as:
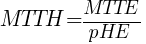 , where MTTE is the mean time to error calculated in the first simulation stage.
, where MTTE is the mean time to error calculated in the first simulation stage.
The final simulation stage requires users to specify a stage 2 simulation result and a number of trials. Each trial is a simulation that begins from a stage 2 event (i.e. hazardous event) and that can lead either to an accident event or to a safe resolution.
When the stage 3 simulation completes, we can calculate the probability of an accident given a hazardous event using the following formula:
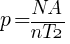 , where NA is the number of accidents generated in stage 3 and nT2 is the number of stage 3 trials.
, where NA is the number of accidents generated in stage 3 and nT2 is the number of stage 3 trials.
This value is used to calculate the mean time to accident:
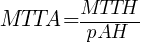 , where MTTH is the mean time to hazard calculated in the previous stage.
, where MTTH is the mean time to hazard calculated in the previous stage.
The statistical confidence of these results depends on the number of trials chosen in each stage. Our software uses a formula that determines a minimum number of trials in each stage required to obtain statistically reliable estimates of accident frequency.
Sample predictions and conclusion
To assess PTC risk, two safety evaluations must be performed: one for a base case scenario where PTC is not installed, and another for an alternate case scenario where PTC is installed. For each scenario we calculate accident frequency, then we compare the results to verify that PTC achieves an 80% reduction in risk.
Here are sample results taken from our publication:
| Level 2 Event | Scenario | Mean Time to Level 2 Event (MTTA) in days |
|---|---|---|
| Work zone accident | Base Alternate |
7,216.98 Over 300 years |
| Head-to-head collision | Base Alternate |
1,596.04 Over 300 years |
| Head-to-tail collision | Base Alternate |
Over 300 years Over 300 years |
| Sideswipe collision | Base Alternate |
414.97 143,130 |
| Emergency brake derailment | Base Alternate |
1,387.65 357,825 |
| Overspeed derailment | Base Alternate |
6,520.12 19,588.42 |
| Misaligned switch derailment | Base Alternate |
463.7 Over 300 years |
| Unauthorized switch derailment | Base Alternate |
482 Over 300 years |
In conclusion, by focusing computer resources only on paths that are likely to lead to accidents, multi-level splitting is an effective simulation technique for predicting rare events. Our simulator can produce a PTC risk analysis in as little as three days and can guarantee high statistical confidence. The PTC-implementing railroads can now conduct speedy analyses to demonstrate the safety of their new PTC systems, and the FRA can trust and approve those technologies to make America’s railroads safer.
- Taken from the Graniteville NTSB accident report. View it here: https://www.ntsb.gov/investigations/summary/RAR0504.html [↩]
- View the NTSB report on the Chatsworth collision here: http://www.ntsb.gov/investigations/summary/RAR1001.html [↩]
- https://www.aar.org/safety/Pages/Positive-Train-Control.aspx#.UlM1y2RgaiI [↩]
- The ideas, formulae, and results detailed in this page are taken directly from our research published in the 2012 Railways issue of the Transportation Research Record: Meyers, T., Stambouli, A., McClure, K., Brod, D. (2012) Risk Assessment of Positive Train Control by Using Simulation of Rare Events. Transportation Research Record, 2289, 34-41 [↩]